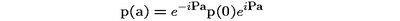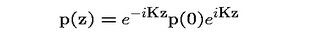Superluminal neutrinos at OPERA. A new model

As promised in the comments section of the previous post, I've completed work on a new model of neutrino superluminality. This paper is now uploaded at http://vixra.org/abs/1201.0091


The idea is that neutrino is not a free particle: it lives in a state of permanent (self-)interaction, which shows up in the form of oscillations between three neutrino types. So, a neutrino should be regarded as a group of three particles, which travel together and periodically change their flavors. Of course, in a relativistically invariant theory the center of energy of this bunch should always move with a constant speed, and for an energetic neutrino this speed should be a bit lower than the speed of light. However, there is no limit on velocities of individual components of the bunch. Positions of these particles can oscillate around the center-of-energy trajectory in concert with the flavor transformation pattern. If averaged over long time, the speed of each component (e.g., mu-neutrino) must be equal to c, but there can be time periods when its speed exceeds the speed of light, and at other times the instantaneous speed can be lower than c.

It is interesting that the amplitude of neutrino position oscillations depends on neutrino masses. For presently known neutrinos with masses around 1 eV/c^2 the magnitude of this effect is estimated to be very small. The suggested solution is to postulate existence of at least one more superheavy neutrino type with the mass of at least 300 MeV/c^2. Then one can easily explain the mu-neutrino position advance of 18 meters observed in the OPERA experiment. This can be seen in the following figure from the paper.



Here L is the neutrino travel distance (in km) and DeltaL is the distance (in meters) between mu-neutrino component and the center-of energy. The curve corresponding to 17 GeV OPERA neutrinos is shown as a broken line. The full line corresponds to MINOS neutrinos with the energy of 3 GeV. From this graph it is clear that MINOS neutrino runs in front of the center-of-energy (i.e., superluminally) up to 1500 km. Then it slows down and runs behind the c.o.e. Beyond 3000 km the neutrino becomes superluminal again, and this pattern is repeated periodically in concert with the mu-tau neutrino oscillation.

SN1987A supernova data (no neutrino superluminality) agree with our predictions quite nicely as well, because neutrino deviations from the light path cannot exceed a few meters, i.e., they are negligible in astronomic observations. The theory also predicts a specific non-linear dependence of the amount of superluminality on neutrino energy and propagation distance. It will be fun to watch how these predictions agree (or disagree) with future neutrino velocity measurements to be performed by the MINOS and OPERA collaborations.

Then what about special relativity, which forbids anything traveling faster than light? This question is answered in the paper as well. As I've said here and here on this blog, simple Lorentz transformations of special relativity are not applicable to interacting systems (such as oscillating neutrinos), so the ban on superluminal velocities does not apply to them.

Superluminal neutrinos at OPERA. Explained.

I haven't touched this blog for a long while, but now it's time for a new post. Everybody knows by now about those neutrinos flying from Switzerland to Italy with superluminal speeds. Most people bet on some experimental blunder commited by the OPERA collaboration. I bet that OPERA results are correct and I have a simple model, which explains where these missing 60 nanoseconds come from. It is a pity that I cannot attach PDF files here, because I have a 20-page paper with the new theory.

To make a long story short, my theory tells that the actual speed of neutrinos is lower than the speed of light (as it should be for any massive particle). Then why do they arrive in the OPERA detector by 60 ns too early? The idea is that neutrinos start their journey from a point, which is 18 meters closer to Italy than everybody thinks.

The funny thing about neutrinos is that they oscillate between three different flavors. In the case of CERN-OPERA neutrinos, one can ignore the electron neutrinos and think only about muon-tau neutrino oscillations. The thing that's even funnier is that neutrinos can oscillate not only between different flavors, but also between different locations in space. The muon neutrino part of the tandem moves along its own trajectory (with the speed of light) and the tau neutrino part moves along a different parallel trajectory (also with the speed of light). The whole system is switching back and forth between the muon flavor and trajectory and the tau flavor and trajectory. The distance between two trajectories can be huge, e.g., 36 meters. Nothing in the theory forbids that.

It is reassuring to check conservation laws: Indeed, the expectation values for the total momentum and the total energy do not change with time. It is also important that in spite of oscillations, the center of energy of this system moves with a constant velocity (=c) along a straight line. This line is in the middle between the muon and tau neutrino trajectories. This is how the free neutrino system looks like.

Next we need to consider the process of neutrino creation at CERN. This happens in meson decays. For example, a pion decays into a muon and a muon neutrino. Everybody thinks that the muon and the neutrino appear from the same point in space (the decay vertex). However, there is absolutely no reason for this to be the case. Moreover, if the above model of neutrino oscillations is correct, then the muon neutrino simply cannot emerge directly from the interaction vertex. In such a case the law of continuity of the center-of-energy trajectory would be violated. So, we get a situation in which the muon part of the neutrino tandem emerges 18 meters from the decay vertex in the forward direction, and the tau part of the tandem is 18 meters behind. Then the muon neutrino arrives in the OPERA detector by 60 ns earlier than expected, while the tau neutrino (not observed in this experiment) is 60 ns late.

This is, basically, my theory. What about the causality violation? Definitely, we have a superluminal signal propagation: neutrinos are created instantaneously 18 meters away from the decay interaction vertex, while according to special relativity it should take them at least 60 ns to get there. Yes, there is superluminal propagation! No, there is no causality violation! The point is that we have an interacting system, therefore boost transformations of observables do not follow usual Lorentz rule, and the usual logic, which "proves" that "superluminality is not causal" does not work here. You can find more details and examples in my book, where I talk about the causality of action-at-a-distance potentials.

Edit: The text of my preprint is now available at http://www.vixra.org/pdf/1110.0052v5.pdf

Infrared infinities and bound states

You can now freely post your comments. Hopefully, those nasty advertisers forgot about my blog by now.


Few months back I promised to deliver a Lamb shift calculation within the dressed particle approach. Well, this appeared to be not so trivial. It was easy to deal with ultraviolet infinities. The dressed particle approach is designed to deal with them. However, the infrared infinities are really nasty. The fundamental point is that in order to use the dressed particle approach one needs to have a well-defined S-operator. It appears that standard QED does not provide a clean S-operator in the presence of massless photons. Strictly speaking, the asymptotic time evolution of colliding electrons is not free due to the long-range Coulomb effects, and the standard scattering theory is not working. The problem is easy to understand: In QED photons are massless, so, the minimum energy to create one photon is zero. When two charges interact, they can easily create an infinite number of "soft" photons. It is impossible to consider a clean interaction of two charges. You should always take into account all those parasitic photons. An infinite number of them!

One known way to deal with this issue is to redefine scattering theory by considering the long-range Coulomb interaction as a part of the free asymptotic Hamiltonian. This has been done by Kulish and Faddeev [1]. Then, one can formally define the S-operator. However, I am still not sure if this presription is unique and if I am allowed to fit my dressed particle Hamiltonian to this redefined S-operator. I had some ideas, but everything started to look so complicated...

I decided to take a simpler route. Let us forget for the moment about those nasty massless photons. There are respectable physical theories where all particles are massive. For example, in theory of nuclear forces one has protons, neutrons, and pions. There is a number of simple QFT models designed to describe nuclear forces. Possibly, the simplest one is the scalar Yukawa model. So, I decided to first apply my approach to this model. There are no infrared problems to worry about.

Of course, I will not get such a clean experimental number as Lamb shift. But getting radiative corrections to nuclear potentials is a worthy goal by itself. Moreover, there are tons of theoretical works in this field to compare with.

That's what I am doing now, i.e., the radiative corrections to the Yukawa potential. The paper is moving ahead rather well, and I don't anticipate any surprising difficulties. I'll keep you posted.


[1] P. P. Kulish and L. D. Faddeev, "Asymptotic conditions and infrared divergences in quantum electrodynamics", Theor. Math. Phys., 4 (1970), 745.

A relativistic quantum theory of gravity

I am happy to announce the release of my new preprint A relativistic quantum theory of gravity. I started this work as a kind of joke: to see whether all relativistic gravitational effects (like the Mercury's perihelion precession and the light bending) can be explained as a consequence of simple two-body potentials acting between particles. Surely, they can. There is no need for curved space-time, general covariance, and other stuff, which manifestly contradicts the ideas of quantum mechanics. So, gravity can be formulated within Relativistic Quantum Dynamics (RQD) similar to electromagnetism. The key ingredient, which enabled this formalism, was the work by Kita who formulated a simple criterion for a two-particle potential to be relativistically invariant.

There was another piece of the puzzle that didn't want to fit and drove me crazy for a week or two. On the one hand, gravity changes the momentum (and energy) of photons. This is clear from the light bending observations. On the other hand, the gravitational time dilation and red shift experimens can be understood only if one assumes that the photon's energy does not change in the gravitational field. I just couldn't understand how these two statements can coexist. Finally, I figured it out. In the red shift experiments one should take into account the full (kinetic + potential) energy of photons, which stays constant in any gravitational field. Indeed, when the photon is absorbed by a detector, all its energy gets absorbed, not just its kinetic energy. Otherwise, the energy conservation law would be violated.
In the light bending situation, the photon's kinetic energy changes together with its momentum. There is not contradiction. Relief.

My next goal is to derive radiative corrections to the Coulomb potential in quantum electrodynamics. The idea is simple. According to RQD, since we know the S-matrix of the renormalized QED, we can fit a dressed particle Hamiltonian to this S-matrix. So, I am going to calculate the S-matrix for the electron-proton scattering up to the one-loop perturbation order (actually, this has been done more than 50 years ago, I just need to reproduce the calculations myself and transfer them to my notation), and then use formulas of RQD to obtain the corresponding electron-proton potential. At the tree-level this is the well-known Breit potentials which describes, in addition to the Coulomb, also magnetic, spin-orbit, and spin-spin interaction. The one-loop correction is supposed to describe the Lamb's shift in the hydrogen atom. So, I need to get this number right. This is going to be the final solution of the bound state problem in quantum field theory. The energies and wave functions of bound states will be obtained from the eigenvalue equation with the dressed particle Hamiltonian, just as in good old quantum mechanics. This should take me a couple of months, if the planets will hold their favorable positions.

About my book

I spent a few months rewriting my book Relativistic Quantum Dynamics. and now I have the 2nd edition out. It is much much better than the 1st edition. One important change is that I separated the book into 2 parts. The first part is largely the traditional theory starting from the principle of relativity and ending with the renormalization in QED. The second part has all the new stuff. I analyze the weak points of QED and show how to fix them. I also spent a lot of efforts to make the book more readable, to correct typos and unavoidable errors (signs, missing factors, etc.) in equations. Comments are appreciated.

Which is the most remarkable and under-appreciated paper about QFT?

Take a look at this paper:

Hideji Kita, A Non-Trivial Example of a Relativistic Quantum Theory of Particles without Divergence Difficulties Prog. Theor. Phys. 35 (1965) 934.


Kita builds a fully relativistic theory of interacting particles without even mentioning quantum fields. This theory doesn't have self-interactions and doesn't require renormalization. Both the Hamiltonian and the boost operator are constructed explicitly. They can be used to calculate the time evolution and boost (Lorentz) transformations of observables to the moving reference frame.

He also translates his theory in the language of quantum fields and explicitly shows how the Haag's theorem works. The "interacting quantum field" does not transform covariantly under boost transformations. (Who cares?)

Unfortunately, this work didn't have any impact on the development of QFT. Now it seems to be completely forgotten.

Kita also had a few follow-up papers in Prog. Theor. Phys. in 1960's and 70's. They are real treats!

What is "dressed particle" approach to QFT?

I promised to tell about it several times. Now is the time.

Recall our discussion of the QED Hamiltonian where we found that the presence of terms like a*c*a makes this Hamiltonian useless for studying the time evolution. The problem was that these terms act non-trivially on 1-particle states. The main idea of the "dressed particle" approach is that there can be no interaction in the vacuum state and in 1-particle states. These states should evolve in time as if there were no interaction at all. Mathematically this requirement means that all terms in the interaction Hamiltonian should have at least two annihilation operators. In order to maintain the Hermiticity, there should be at least two creation operators in each interaction term. So, in a theory of interacting electrons and photons, the simplest normally ordered terms allowed in the interaction Hamiltonian are

a*a*aa
a*c*ac
a*a*c*aa
a*a*a*aaa
...

The first term here describes a direct electron-electron interaction; the second term is an electron-photon potential responsible for the Compton scattering; the third term describes bremsstrahlung, i.e., emission of photons in electron-electron collisions; the fourth term is a three-body electron-electron-electron potential,...

It is important that all these terms yield zero when acting on the vacuum and 1-particle states. This means, for example, that the electron mass is not affected by interaction, so there is no need for renormalization.

As I mentioned here , a number of relativistically invariant and cluster separable models of this sort were constructed by H. Kita. There is also a "dressing approach" by Greenberg and Schweber which allows one to make a "dressed particle" theory out of virtually any usual QFT. What is really exciting is that this approach works and one can construct a "dressed" version of QED and other popular theories. This provides a completely new perspective on foundations of relativistic quantum physics.

Weinberg's book

If you are interested in QFT, I strongly recommend you to read Weinberg's book [1]. It is so much different from all other books on the subject. Weinberg does not pretend that the idea of quantum fields arises from "generalization" of quantum-mechanical wave functions or as a quantum version of classical field theory. In Weinberg's book you will not find rather dubious logical chains like "Schroedinger equation -> Dirac equation -> Dirac's hole theory -> QFT" or "Lagrangian -> Klein-Gordon equation -> quantization -> quantum fields". His approach to quantum fields, Lagrangians, and gauges is pretty utilitarian.

Weinberg correctly says that the only thing we are interested in QFT is the S-matrix. We want the S-matrix to be (at least) relativistically invariant and cluster separable. This implies that the Hamiltonian of the theory should be relativistically invariant and cluster separable. He goes on to demonstrate how Hamiltonians with these properties can be constructed as certain polynomials of operator functions defined on the Minkowski space-time. These operator functions are called quantum fields and they are required to satisfy some formal properties, like (anti-)commutativity at space-like intervals and covariant Lorentz transformation laws. The fact that quantum fields satisfy Klein-Gordon or Dirac equations is almost accidental, and has no any fundamental significance.

In Weinberg's logic, there is no reason to assume that quantum fields have any physical interpretation. They are just formal mathematical constructs. Moreover, there is no reason to associate the Minkowski space-time on which the fields "live" with real physical space and time.

This is by far the best book written about QFT. It gives you a very clear and, in my opinion, the only correct perspective on the foundations of QFT. Enjoy reading!

[1] S. Weinberg, The Quantum Theory of Fields, Vol. 1 , (University Press, Cambridge, 1995)

What are quantum fields?

Relativistic QFT is a fine theory. If you hold your nose and follow textbook recipes without asking too many questions, you can finally calculate a lot of stuff (scattering cross-sections, Lamb shifts, etc.) in a remarkable agreement with experiment.

However, on this blog we are going to ask questions. Why not? For example:

• Q: What are quantum fields?
• A: They are operator functions on the Minkowski space-time.
• Q: What is their physical meaning?
• A: They are obtained by second quantization of wave functions, at least in the non-interacting theory.
• Q: Wave functions have probabilistic interpretation, and in a relativistic theory the probabilities must be invariant with respect to Poincare transformations. Is it true?
• A: Yes.
• Q: Then particle wave functions must transform by a unitary representation of the Poincare group. Right?
• A: Right.
• Q: So, if quantum fields (even non-interacting) are somehow related to particle wave functions, they also must transform unitarily. Right?
• A: That sounds plausible.
• Q: However, this is not true. Take, for example, Dirac field for electrons. Lorentz transformations of this field are represented by 4x4 matrices. However, it is well-known that there are no finite-dimensional unitary representations of the non-compact Lorentz group. So, Lorentz transformations of the Dirac field are non-unitary.
• A: So what?
• Q: This means that there is no direct connection between the electron's quantum field and electron's wave function?
• A: I am not sure.
• Q: In the quantum field ψ(x,t) the argument x is physical position and t is time. Isn't it?
• A: Yes.
• Q: Is it possible to think (as we do in quantum mechanics) that x as an eigenvalue of the position operator?
• A: I guess so.
• Q: Then we should accept the existence of the time operator as well, which is impossible .
• A: Why did you make this conclusion?
• Q: Because the Lorentz transformation of the field ψ(x,t) involves intermixing of the arguments x and t, which is only possible if x and t are eigenvalues of operators X and T that do not commute with the boost generator.
• A: I guess you may be right.
• Q: So, there is no connection between quantum field and quantum-mechanical wavefunctions. And quantum fields are just abstract operator functions on an abstract 4-dimensional space whose coordinates are not necessarily related to experimentally observed positions and times.
• A: Why do you call Minkowski space-time "abstract"?
• Q: We will talk about Minkowski space-time later. However, arguments x and t of quantum fields are just dummy integration variables without any particular physical meaning.
• A: Why it is so?
• Q: Because, as we discussed here, the only physical thing predicted by relativistic QFT is S-matrix. And in the expression for the S-matrix quantum fields enter integrated over x and t. All dependence on x and t is lost.

P.S. Everything said above refers only to relativistic quantum fields used in theories like QED. They should be separated from non-relativistic quantum fields used, for example, in condensed matter physics. The quantum field of phonons is a well-defined operator which is related to displacements of real atoms from lattice positions.

How we can improve QED?

Let us now count arguments for and against the currently accepted form of the renormalized QED. We start with positive things:

1. QED is relativistically invariant
2. QED is cluster separable
3. The S-matrix of QED perfectly agrees with experiment.

Now the negatives:

1. The Hamiltonian of QED contains infinite counterterms
2. QED interaction leads to unphysical processes of creation and absorption of extra particles from vacuum and 1-particle states
   

Is it possible to reformulate the theory so as to keep the positive stuff and get rid of the negative? Yes. The answer is here. The Hamiltonian of QED is apparently wrong, but according to Ekstein, we can modify the Hamiltonian without changing the S-matrix (i.e., without changing the agreement with experiment). This can be done by a unitary transformation. Moreover, if we are careful enough, we can choose this transformation such that both the relativistic invariance and the cluster separability are not affected. Now, the question is, whether one can simultaneously eliminate bad properties 1. and 2? And the answer is, again, 'yes'! One can find a unitary transformation of the Hamiltonian such that all interaction terms become finite, and all terms that act non-trivially on the vacuum and 1-particle states are eliminated. In one shot we kill two rabbits: with the new Hamiltonian the renormalization is not needed anymore and we have a clean physically satisfactory definitions of the vacuum and 1-particle states. This is called the "unitary dressing transformation". More about it in another post.

Update So, the conclusion is that the QED Hamiltonian is simply wrong and must be substituted by another Hamiltonian. Why did we use a wrong Hamiltonian for almost 80 years? One reason is in three "good" properties I listed above. This is a respectable reason. Another reason is that the Hamiltonian of QED was derived from correspondence with classical Maxwell's theory of electromagnetism. This is, actually, not a good reason. As we discussed here , Maxwellian description of radiation by a continuous wave is not accurate. There are numerous other flaws in Maxwell's theory, one of them being inadequate description of the "radiation reaction" force. So, derivation of quantum electrodynamics by "quantizing" classical theory is, at best, a heuristic trick.

What's wrong with the Hamiltonian of QED?

I mentioned several times on this blog that the non-trivial action of the QED interaction V on the vacuum and one-particle states is deeply disturbing. What's wrong with it?

The interaction Hamiltonian V written in terms of particle creation and annihilation operators contains so-called tri-linear terms. An example of such a term is the product of three particle operators a*c*a, where I denoted 'a*' an electron creation operator, 'a' an electron annihilation operator, and 'c*' a photon creation operator. Let us focus just on this term and write the full Hamiltonian H in the truncated form (all momentum, spin, and polarization labels are omitted as well as numerical factors, integration signs, etc.)

H = H_0 + a*c*a + ... (1)

Having the full Hamiltonian H one can form the time evolution operator U = exp(iHt) and study the time dependence of states and observables. Let us consider the time evolution of a state a*|0> which at time t=0 had only one electron (here |0> denotes the vacuum state). We would expect (according to observations) that a single electron always remain in the one-electron state. Let us now find out whether this expectation is fulfilled with our Hamiltonian. We are going to find out how this state will look like after short time t. Let us take t small enough, so that the time evolution operator U can be approximated by linear terms in the series over t. Then

exp(iHt) a*|0> = exp(it(H_0 + a*c*a + ...)) a*|0>
= (1 + it H_0 + it a*c*a + ...) a*|0>
= a*|0> +it H_0 a*|0> + it a*c*a a*|0> + ... (2)

The first two terms in this expansion are harmless. They both correspond to states with one electron, as expected. However, the third state is different. After bringing the particle operators to the normal order and omitting, again, all numerical factors, this term will look like

a*c*|0> (3)

and this is now a state with one electron and one photon. So, the time evolution with the QED Hamiltonian (1) leads to the "emission" of photons by a single free electron. Such an effect has never been seen experimentally. The problem becomes even more severe if we take more terms in the expansion of the operator U and consider additional terms in the interaction V. It is easy to show that the vacuum state |0> will also become unstable with respect to the decay into multiparticle states containing photons and electron-positron pairs. This is also unphysical.

The cure for this desease is known for many years. It is often said that creation and annihilation operators, like a* and a, do not correspond to real physical particles. They describe creation and annihilation of fictitious "bare" particles. Real electrons are complex linear combinations of multiparticle "bare" states. Although, this has been known for decades, there were suprisingly few attempts to reformulate QED in terms of physical particles that can be observed. In view of the complete failure of QED to describe the time evolution, such reformulation of the theory seems to be a reasonable step. This step is exactly the essence of the "dressed article" program initiated in 1958 by the work of Greenberg and Schweber [1].

I would like to mention just one more thing. It appears that in a properly dressed theory all ultraviolet divergences disappear from both the S-matrix and the Hamiltonian. More about the "dressed particle" approach in later posts.

[1] O. W. Greenberg and S. S. Schweber, "Clothed particle operators in simple models of quantum field theory", Nuovo Cim., 8, (1958) 378.

How we can improve QFT?

Here we discussed that QFT in its current form cannot describe the time evolution of wave functions and observables. Here we quoted Weinberg as saying that QFT is the only way to unify relativity with cluster separability and that any fundamental theory in the low-energy limit should look like QFT. So, what shall we do now? Give up? No.

It appears that Weinberg's profesy is wrong. There is a way to construct a low-energy fundamental relativistic quantum theory that does not look like QFT. Examples of such theories were constructed by Kita in [1] and in several later papers. Similar ideas were explored by Kazes [2]. By following these approaches, one can define interaction operators in H = H_0 + V and K = K_0 + W (see here ) so that (i) the Poincare commutators are satisfied, (ii) the interaction operators are cluster separable, (iii) V and W yield zero when acting on the vacuum and 1-particle states. The last condition is important to have a well-defined time evolution in the theory.

The bad news about Kita's theory is that he was able to construct only simple models that apparently have no counterparts in nature. The good news is that his approach can be applied to realistic theories, such as QED. A satisfactory version of QED with properties (i), (ii), and (iii) can be constructed by using the "dressed particle" approach. More about that in another posting.



[1] H. Kita, "A non-trivial example of a relativistic quantum theory of particles without divergence difficulties", Progr. Theor. Phys., 35, (1966) 934.

[2] E. Kazes, "Analytic theory of relativistic interactions", Phys. Rev. D, 4, (1971) 999.

Is there an observable of time?

We already discussed here, here, and here that the principle of relativity does not require the symmetry between space and time coordinates alleged in Einstein's special relativity. Here I would like to suggest another argument for the deep division between time and position. The point is that position is an observable, while time is not.

When we measure position of a particle or any other physical system, we know that the result of measurement will depend on the state of the observed system.
In quantum mechanics there is an Hermitian operator corresponding to position, and observations of the position are normally associated with uncertainties that are characteristic to measurements of quantum observables.

Time is different. Time is "measured" by simply looking at the wall clock in the laboratory. The value of time does not depend on what physical system is actually observed and what is the state of the system. The value of time would be just the same if we haven't observed any physical system at all. So, time is simply a classical parameter associated with the act of measurement. We perform a measurement of some observable and we attach to this measurement a numerical label called "time". This label belongs to the same class as nine other labels that should be attached to each measurement. These are labels that uniquely specify the reference frame in which the measurement was made: its position, orientation, and velocity. So, time is just one of the 10 parameters of the reference frame or laboratory, and time has nothing to do with the properties of the physical system that may be (or may be not) present in the laboratory.

So, it is not surprising that there is no operator of time in quantum mechanics. (Some published attempts to introduce such an operator do not look convincing.) This observation is just another reason to stop using the Minkowski space-time formalism in relativistic theories.

What is observable and what is not?

In physics, there are some things that can be directly observed by experiment, and there are other things that exist only in theories and are not observable. The things of the first kind are, for example, various properties of particles, such as mass, spin, momentum, position, etc. There are lot of experimental devices which measure these properties directly: beginning from simple rulers and ending with Wilson chambers and Stern-Gerlach apparatuses. Examples of things of the second kind (non-observable) are fields and space-time.

Take for example, the electromagnetic field. There is no way one can directly measure the strength of the field (electric or magnetic) at a given point. All we can do is to place a test charge at this point and measure the force acting on this charge. One is free to think that this force appears because of the non-zero field vector created at this point by other charges. However, one can also think that there is no field and the force is simply created by action-at-a-distance from the surrounding charges. In classical electrodynamics, one also assigns certain momentum (density) and energy (density) to the fields. In the case of static fields this momentum-energy is certainly non-observable. In the case of freely propagating transversal field (= light wave) the momentum-energy can be equally well assigned to the particles of light - photons (see also discussion here ). So, the idea of electromagnetic field as a separate physical entity is somewhat suspicious.

Now consider the space-time. In modern theories the space-time is an active participant in physical processes. It can be bent, twisted, torn... It even has momentum-energy associated with it (with the "gravitational field"). However, nobody can see the space-time properties directly. What we actually see in experiments are trajectories of particles, i.e., the time dependent expectation values of the position observable r(t). These trajectories can be calculated in the Hilbert space formalism of quantum mechanics, where the notion of space-time is just not needed.

I believe that a successful physical theory should be formulated (as much as possible) in terms of directly observable quantities (= particle properties described above). I strongly believe that current crisis in theoretical physics in large part is related to our focus on abstract theoretical non-observable notions, such as fields and space-time.

Can relativistic QFT predict time evolution?

From what I know about relativistic quantum field theory, the answer is "no" (if you disagree, please provide a reference that proves otherwise). The explanation is simple. In quantum mechanics, one needs to have a well-defined Hamiltonian in order to form the time evolution operator exp(iHt) and to calculate the time dependence of wave functions and observables. However, in relativistic QFT, the only sensible Hamiltonians (i.e., those that can be used to calculate the S-matrix via Feynman-Dyson formula) must contain infinite renormalization counterterms. So, they are not well-defined. They are actually not defined at all. Even if we forget about the infinities in QFT Hamiltonians (for example, we can introduce artificial momentum cutoffs), they are still not good, because they normally contain terms (like trilinear terms in QED) which have a non-trivial action on the vacuum and one-particle states. This is completely at odds with the observed stability of vacuum and single particles.

QFT is good at calculating one and only one thing - the S-matrix (or the S-operator). All wonderful experimental predictions of QED or Standard Model (scattering amplitudes, anomalous magnetic moments, Lamb shifts, etc.) are related to the S-matrix elements. The time evolution enters in the S-matrix in an integrated form (from infinite past to infinite future). It is just impossible to recover the detailed form of a function by knowing its definite integral. By having exact knowledge about the S-operator we can say very little about the underlying Hamiltonian. It has been shown [1] that there exists a huge class of scattering-equivalent Hamiltonians connected to each other by unitary transformations.

So, the great successes of relativistic renormalized QFT in calculations of the S-matrix and related observable quantities do not at all contradict the miserable performance of QFT when it comes to calculations of the time evolution. This fact went unnoticed for a long time for a simple reason. Currently there are no experimental techniques capable of measuring the detailed time evolution of micro-particles. Existing time-dependent experimental data are of such a low quality that simple non-relativistic Hamiltonians are quite capable to describe them, and fine relativistic and radiative corrections are just not needed.

There is a way to fix this problem, i.e., to have a finite well-defined Hamiltonian which is useful for both S-matrix and time evolution calculations in QFT. This way is called the dressed particle approach. More about that in another posting.

[1] H. Ekstein, "Equivalent Hamiltonians in scattering theory", Phys. Rev. 117 (1960), 519

What is the meaning of relativistic invariance?

It is usually assumed that in order to be relativistically invariant a physical theory must be formulated in terms of manifestly covariant quantities, i.e., quantities that transform as scalars, vectors, tensors, etc. with respect to boost transformations. For example, relativistic quantum theories of single particles were initially formulated by using wave equations (Klein-Gordon, Dirac, etc.) in which the time and position variables were formally equivalent. We already discussed that the tensor transformation laws of observables and the formal equivalence of the time and position coordinates are approximations. Then what is the exact meaning of relativistic invariance? How one can say whether a theory is relativistically invariant or not?

The key to understanding the relativistic invariance is not in the formal equivalence of space and time coordinates. The key is in the (Poincare) group properties of the ten types of inertial transformations (1 time translation, 3 space translations, 3 rotations, and 3 boosts). A quantum theory if fully relativistic if there is an unitary representation of the Poincare group in the Hilbert space of the system, and if the generators H for time translations, P for space translations and J for spatial rotations of this representation are identified with the observables of the total energy, total momentum and total angular momentum, repsectively, of the system. A relativistic classical theory is defined similarly. The difference is that instead of the "Hilbert space" one should use the "phase space", and instead of "unitary transformations" one should use "contact transformations", i.e., those conserving the Poisson brackets.

Is interference a quantum effect?

Consider the famous double-slit experiment with photons. This experiment can be performed in two regimes: the low intensity (Feynman) regime and the high intensity (Young) regime. In the Feynman regime, photons are released one-by-one, the image on the screen is built one dot at a time, and the explanation of the interference picture is given by quantum mechanics of particles - photons. In the Young regime, the interference picture is exactly the same as in the Feynman regime (after enough dots were accumulated on the screen, so that a continuous distribution of the intensity emerged), however, the explanation of the interference is radically different. Classical electrodynamics describes light as a continuous electromagnetic field. One interference picture, two different explanations. Which one is correct?

Note that there is no any significant difference between these two regimes apart from the intensity of light or the number of emitted particles. Therefore it would be not correct to say that the Young regime arises in some kind of classical limit, i.e., when the Planck constant can be neglected. The same physical mechanism works in both regimes, and the theoretical explanation should be also the same. The only explanation that works in both cases is the view that light is a flow of particles - photons, and that the wave properties of light are manifestations of the quantum nature of these particles.

This brings up interesting questions. Are we making a mistake when calling Maxwell's wave theory of light a "classical theory"? Is wave theory of light, in fact, a surrogate attempt to describe quantum effects? I think the answers to both these questions should be "yes". Newton's rings, Grimaldi's diffraction, and Young's interference are genuine quantum effects, and their correct description requires the machinery of quantum mechanics: Hilbert spaces, wave functions, etc.

Newtonian ray optics in which light corpuscles move along well-defined trajectories is the only truly classical description of light.

Are different forms of relativistic dynamics physically equivalent?

The concept of the form of dynamics was introduced by Dirac in 1949 [1]. Any quantum relativistic system is described by a Hilbert space in which there is a unitary representation of the Poincare group. This representation has 10 Hermitian generators: time translations are generated by the Hamiltonian H, space translations are generated by the vector of the total momentum P, rotations are generated by the vector of the total angular momentum J, and boosts are generated by the vector of boost K. In an interacting theory, some of these generators may be interaction-dependent, while others are interaction-free. The different choices of interacting generators are called different "forms of dynamics", according to Dirac. There is a wide-spread opinion that different forms of dynamics are physically equivalent. Here I would like to show that this opinion is not correct.

First consider the instant form of dynamics in which only the Hamiltonian H and the boost operator K have interaction contributions V and W, respectively

Let us now see how certain observables transform with respect to space translations. Consider the momentum operator p of one particle in the system. Denote p(0) the operator corresponding to the initial reference frame, and p(a) the momentum operator in the reference frame translated by the distance a. Then, basic rules of quantum mechanics tell us that

(1)

In the instant form of dynamics p(0) commutes with P, so particle's momentum is not affected by the translation of the observer. This is exactly what we observe in nature.

Now, let us take up the case of the point form of dynamics. The characteristic property of this form is that the Hamiltonian H and the total momentum operator P contain interaction terms, while J and K are the same as in the non-interacting theory.

If we now apply space translation (1) to the momentum operator of the particle and take into account that normally interaction Z does not commute with p(0), we will see that space translations change the observed values of the particle's momentum. In other words, the measurement of momentum depends on the distance between the observer and the observed particle. Such a behavior has never been seen in experiment. Therefore, the point form of dynamics is ruled out.

It is true that the S-matrix does not depend on which form of dynamics is used in calculations. This explains successful applications of different forms of dynamics (e.g., the point form and, especially, the front form) in calculations of scattering and energies of bound states in nuclear physics. But this is an entirely different matter, and I will discuss it in a different post. The conclusion of this post is: different forms of dynamics are scattering equivalent, but they are not physically equivalent.

[1] P. A. M. Dirac, Forms of relativistic dynamics , Rev. Mod. Phys., 21 (1949), 392.

Is there Minkowski space-time?

The issue of the non-universality and interaction-dependence of Lorentz transformations was discussed here and here . It was shown that in a rigorous quantum relativistic setting, the Lorentz transformations (for the energy-momentum of particles as well as for the position-time of events) depend on the interaction acting in the physical system. The boost transformations of particle observables are sensitive to the presence of other particles around and on interactions with them.

This means that one cannot rigorously introduce the idea of Minkowski space-time. Indeed, this idea works only in the case when all physical systems obey exactly the same boost transformation laws - the Lorentz transformations. Only then one can say that these are not simply transformations of individual particle observables, but global transformations of space-time coordinates (similar to universal and interaction-independent spatial shifts and rotations). This is the story told to us by Einstein's special relativity, and this is an old story that should be changed.

• Q.: Are you saying that particle observables, such as momentum and energy, do not transform according to covariant tensor laws?
• A.: Yes.
• Q.: Then how do they transform when the velocity of the observer changes?
• A.: The exact transformation laws are very close to the usual Lorentz formulas, but they include small corrections that depend on the state of the system of particles and on the interaction acting there. There is no universal formula.
• Q.: Can you say something more definitive?
• A.: Yes, I can. One can perform a rigorous calculation of the slowing down of the decay of fast moving particles and show that Einstein's time dilation formula holds only approximately.
• Q.: But this formula was confirmed in particle decay experiment to a great precision.
• A.: It is true. However, the corrections to the decay laws of moving particles predicted by my approach are several orders of magnitude smaller than the resolution of modern instruments.
• Q.: I find it difficult to believe that the Minkowski space-time picture that served us well for almost 100 years should be abandoned. A huge part of theoretical physics is built upon this formalism.
• A.: Let me give you one more argument. Please compare two kinds of inertial transformations: time translations and boosts. It doesn't look surprising that the result of a time translation is interaction-dependent. The time evolution of an interacting system is quite different from the time evolution of a non-interacting system. Why boosts should be different? In the instant form of Dirac's dynamics, the boost operator (just like the Hamiltonian) is interaction-dependent. Therefore we should expect that boost transformations of observables in the interacting system should be different from the transformations in the non-interacting system. There is a full analogy with the time evolution.
• Q: If we abandon the Minkowski space-time and covariant tensor transformation laws, then there is nothing left from the theory of relativity.
• A: I do not agree. The theory becomes more complicated than Einstein's special relativity with universal space-time. This is true. However, the most important ingredient of any relativistic theory is not affected: the invariance of physical laws with respect to the Poincare group of inertial transformations is strictly maintained. Together with the laws of quantum mechanics, this is sufficient for performing all kinds of quantum relativistic calculations.

More about the (non-)universality of Lorentz transformations

In a previous post we discussed Lorentz transformations in special relativity. We established that there are no a priori reasons why these transformations should be considered exact and universal.

Here is another argument showing that Lorentz transformations actually cannot be exact and universal. Consider any relativistic quantum theory (QFT, for example). In the Hilbert space of the system there should be an unitary representation of the Poincare group with ten generators

(see, for example, [1], eqs. (3.3.18) and (3.3.20)). Note that the presence of the interaction term W in the boost operator K is absolutely required in order for the theory to be relativistically invariant, i.e., in order to maintain the Poincare commutation relations between generators H, P, J, K.

The operator K generates boost transformations of observables. So, if p(0), for example, is the momentum of one particle in the reference frame at rest, then the momentum of this particle in the moving reference frame is given by

(1)


where z is the rapidity of the boost. Now it is easy to see that if in formula (1) we use the non-interacting boost operator (with W=0), then it leads exactly to the familiar Lorentz formula for momentum-energy. So, Lorentz transformations are definitely applicable to non-interacting systems of particles.

However, if in eq. (1) we use the full interacting boost operator K, then the boost transformation is different from the simple linear Lorentz formula, because operator W generally does not commute with p(0). Thus, momentum-energy boost transformations of interacting particles depend on interaction. This demonstrates that universal interaction-independent Lorentz transformations contradict relativity (=the Poincare group properties) and quantum mechanics.

[1] S. Weinberg, The Quantum Theory of Fields vol. 1 (1995)

Are Lorentz transformations exact and universal?

Textbook presentations of special relativity usually start from two Einstein's postulates:

• Postulate 1 (the principle of relativity): All inertial frames of reference are equivalent.
• Postulate 2 (the invariance of the speed of light): The speed of light is the same for all observers and does not depend of the speed of the source.

Then the textbook discusses various physical events usually associated with light pulses. For such events one can use the Postulate 2 and derive the beautiful results of special relativity: the time dilation, the length contraction, the relativity of simultaneity, etc. All these results are summarized in the Lorentz transformations for the time and position of events. All this is fine and good.

The problems begin when one wants to extend the Lorentz transformations and other special-relativistic formulas to events associated not with light pulses, but with systems of interacting particles. How can we do that? There is no Postulate telling us anything about interacting particles. So, when we say that Lorentz transformations apply universally to all events and phenomena in the world, we make a huge leap of faith. Actually, we introduce into special relativity a third Postulate

• Postulate 3 (the universality of Lorentz transformations) The Lorentz transformations of special relativity apply to all events independent on their nature and involved interactions.

Only after this Postulate is introduced, we can notice the suspicious symmetry between spatial and temporal coordinates of events and how they transform to the moving frame of reference. Only then we can follow Einstein and Minkowski and boldly introduce the idea of space-time unification into one 4-dimensional continuum.

The question I would like to ask is this: What is the reason for introducing this third (hidden) Postulate? Yes, I know how well special relativity agrees with experiment. However, it could be possible that one can abandon Postulate 3 and still keep this perfect agreement with experiment. Actually, this is possible. One can construct a theory in which Postulates 1 and 2 are respected, but Postulate 3 is not. In this theory, therefore, there is no place for the 4D Minkowski space-time. In this theory, the Lorentz transformations are violated by a tiny amount that depends on the strength of interaction acting in the physical system. These violations are, in principle, observable. However, they are a few orders of magnitude less than the resolution of modern instruments. More about that in later posts.

What is QFT?

In 1997 Steven Weinberg published a fascinating little article What is Quantum Field Theory, and What Did We Think It Is? On 17 pages he managed to give three totally different definitions of Quantum Field Theory ...and I quote:

1. "The bottomline is that quantum mechanics plus Lorentz invariance plus cluster decomposition implies quantum field theory." This suggests to me that QFT is just a mathematical formalism that allows one to satisfy these three respectable principle. It is not prohibited to look for other formalisms that satisfy the same principles. Weinberg himself says that there is no proof that QFT is the only option.
2. "In its mature form the idea of quantum field theory is that quantum fields are the basic ingredients of the universe, and particles are just bundles of energy and momentum of the fields." Probably I was wrong, and there is no way around fields. Fields rule!
3. "The present educated view of the standard model, and of general relativity, is again that these are leading terms in effective field theories." Translation: quantum field theory is not fundamental. QFT is simply a low-energy approximation to some truly fundamental theory. Needless to say that nobody has a clue what this truly fundamental theory is.

Which of these three statements is (more) correct? "Bottomline", "mature form", or"educated view"? I'll tell you my opinion in another post.

Hello world!

• Q: What is the point of opening this blog?
• A: I would like to discuss here some fundamental problems in theoretical physics.
• Q: Like what?
• A: What is Minkowski space-time? Can one modify quantum mechanics? What are quantum fields? Is renormalization necessary? Is Maxwell's theory an accurate description of classical electrodynamics? What is the meaning of the gauge invariance?
• Q: Isn't it easier to pick up a textbook and find the answers there?
• A: Yes, if you believe that textbooks give you complete and precise answers. I have some doubts about that. I believe there are grey areas and lots of unanswered questions.
• Q: Why do you think these issues are important?
• A: It is not a secret that modern theoretical physics is in crisis. I believe that we cannot move forward without full understanding of foundational questions.
• Q: Crisis?.. What crisis!? Do you know about the Standard Model and Einstein's General Relativity which precisely describe all observable phenomena?
• A: Yes, I know about impressive results of these theories. However, I also know about some flaws and inconsistencies there. I would like to discuss them at this blog.
• Q: Are you going to offer a solution to the problem of quantum gravity?
• A: I have some ideas about that. However, I think, before moving into that territory it is important to reexamine the foundations: Special Relativity, Quantum Mechanics, and their unification.
• Q: What is the point of doing that? Very smart people worked on these issues for more than 100 years. Everything that can be solved and understood is already solved and understood. Special Relativity and Quantum Mechanics are happily united in Quantum Field Theory and, ultimately, in the Standard Model.
• A: Well, if everything is so cool, then why the unification of SM and GR is such an intractable problem? Something should be wrong in our present understanding of Nature. Let us review what has been done in the last 100 years. Maybe we will find some unexplored areas and some new ways of looking at things.
• Q: What do you think about string theory?
• A: No comments.
• Q: What do you think about loop quantum gravity?
• A: No comments.
• Q: What do you think about Axiomatic (Algebraic) QFT?
• A: No comments.