More about the (non-)universality of Lorentz transformations
Here is another argument showing that Lorentz transformations actually cannot be exact and universal. Consider any relativistic quantum theory (QFT, for example). In the Hilbert space of the system there should be an unitary representation of the Poincare group with ten generators

(see, for example, [1], eqs. (3.3.18) and (3.3.20)). Note that the presence of the interaction term W in the boost operator K is absolutely required in order for the theory to be relativistically invariant, i.e., in order to maintain the Poincare commutation relations between generators H, P, J, K.
The operator K generates boost transformations of observables. So, if p(0), for example, is the momentum of one particle in the reference frame at rest, then the momentum of this particle in the moving reference frame is given by
(1)
where z is the rapidity of the boost. Now it is easy to see that if in formula (1) we use the non-interacting boost operator (with W=0), then it leads exactly to the familiar Lorentz formula for momentum-energy. So, Lorentz transformations are definitely applicable to non-interacting systems of particles.
However, if in eq. (1) we use the full interacting boost operator K, then the boost transformation is different from the simple linear Lorentz formula, because operator W generally does not commute with p(0). Thus, momentum-energy boost transformations of interacting particles depend on interaction. This demonstrates that universal interaction-independent Lorentz transformations contradict relativity (=the Poincare group properties) and quantum mechanics.
[1] S. Weinberg, The Quantum Theory of Fields vol. 1 (1995)
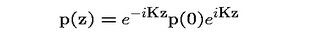


0 Comments:
Post a Comment
<< Home