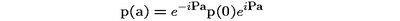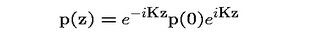Are different forms of relativistic dynamics physically equivalent?
First consider the instant form of dynamics in which only the Hamiltonian H and the boost operator K have interaction contributions V and W, respectively

Let us now see how certain observables transform with respect to space translations. Consider the momentum operator p of one particle in the system. Denote p(0) the operator corresponding to the initial reference frame, and p(a) the momentum operator in the reference frame translated by the distance a. Then, basic rules of quantum mechanics tell us that
(1)
In the instant form of dynamics p(0) commutes with P, so particle's momentum is not affected by the translation of the observer. This is exactly what we observe in nature.
Now, let us take up the case of the point form of dynamics. The characteristic property of this form is that the Hamiltonian H and the total momentum operator P contain interaction terms, while J and K are the same as in the non-interacting theory.
If we now apply space translation (1) to the momentum operator of the particle and take into account that normally interaction Z does not commute with p(0), we will see that space translations change the observed values of the particle's momentum. In other words, the measurement of momentum depends on the distance between the observer and the observed particle. Such a behavior has never been seen in experiment. Therefore, the point form of dynamics is ruled out.
It is true that the S-matrix does not depend on which form of dynamics is used in calculations. This explains successful applications of different forms of dynamics (e.g., the point form and, especially, the front form) in calculations of scattering and energies of bound states in nuclear physics. But this is an entirely different matter, and I will discuss it in a different post. The conclusion of this post is: different forms of dynamics are scattering equivalent, but they are not physically equivalent.
[1] P. A. M. Dirac, Forms of relativistic dynamics , Rev. Mod. Phys., 21 (1949), 392.